From Wikipedia, the free encyclopedia
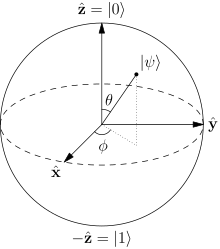
The Bloch sphere is a representation of a qubit, the fundamental building block of quantum computers.
Although quantum computing is still in its infancy, experiments have been carried out in which quantum computational operations were executed on a very small number of qubits (quantum bits).[6] Both practical and theoretical research continues, and many national governments and military funding agencies support quantum computing research to develop quantum computers for both civilian and national security purposes, such as cryptanalysis.[7]
Large-scale quantum computers will be able to solve certain problems much faster than any classical computer using the best currently known algorithms, like integer factorization using Shor's algorithm or the simulation of quantum many-body systems. There exist quantum algorithms, such as Simon's algorithm, which run faster than any possible probabilistic classical algorithm.[8] Given sufficient computational resources, a classical computer could be made to simulate any quantum algorithm; quantum computation does not violate the Church–Turing thesis.[9] However, the computational basis of 500 qubits, for example, would already be too large to be represented on a classical computer because it would require 2500 complex values (2501 bits) to be stored.[10] (For comparison, a terabyte of digital information is only 243 bits.)
Contents
Basis
A classical computer has a memory made up of bits, where each bit represents either a one or a zero. A quantum computer maintains a sequence of qubits. A single qubit can represent a one, a zero, or any quantum superposition of these two qubit states; moreover, a pair of qubits can be in any quantum superposition of 4 states, and three qubits in any superposition of 8. In general, a quantum computer with qubits can be in an arbitrary superposition of up to
qubits can be in an arbitrary superposition of up to 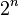 different states simultaneously (this compares to a normal computer that can only be in one of these
different states simultaneously (this compares to a normal computer that can only be in one of these 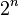 states at any one time). A quantum computer operates by setting the
qubits in a controlled initial state that represents the problem at hand
and by manipulating those qubits with a fixed sequence of quantum logic gates. The sequence of gates to be applied is called a quantum algorithm.
The calculation ends with measurement of all the states, collapsing
each qubit into one of the two pure states, so the outcome can be at
most
states at any one time). A quantum computer operates by setting the
qubits in a controlled initial state that represents the problem at hand
and by manipulating those qubits with a fixed sequence of quantum logic gates. The sequence of gates to be applied is called a quantum algorithm.
The calculation ends with measurement of all the states, collapsing
each qubit into one of the two pure states, so the outcome can be at
most  classical bits of information.
classical bits of information.An example of an implementation of qubits for a quantum computer could start with the use of particles with two spin states: "down" and "up" (typically written
 and
and  , or
, or 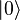 and
and  ). But in fact any system possessing an observable quantity A, which is conserved under time evolution such that A has at least two discrete and sufficiently spaced consecutive eigenvalues, is a suitable candidate for implementing a qubit. This is true because any such system can be mapped onto an effective spin-1/2 system.
). But in fact any system possessing an observable quantity A, which is conserved under time evolution such that A has at least two discrete and sufficiently spaced consecutive eigenvalues, is a suitable candidate for implementing a qubit. This is true because any such system can be mapped onto an effective spin-1/2 system.Bits vs. qubits
A quantum computer with a given number of qubits is fundamentally different from a classical computer composed of the same number of classical bits. For example, to represent the state of an n-qubit system on a classical computer would require the storage of 2n complex coefficients. Although this fact may seem to indicate that qubits can hold exponentially more information than their classical counterparts, care must be taken not to overlook the fact that the qubits are only in a probabilistic superposition of all of their states. This means that when the final state of the qubits is measured, they will only be found in one of the possible configurations they were in before measurement. Moreover, it is incorrect to think of the qubits as only being in one particular state before measurement since the fact that they were in a superposition of states before the measurement was made directly affects the possible outcomes of the computation.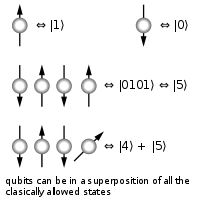
Qubits are made up of controlled particles and the means of control
(e.g. devices that trap particles and switch them from one state to
another).[11]
 different three-bit strings 000, 001, 010, 011, 100, 101, 110, 111. If it is a deterministic computer, then it is in exactly one of these states with probability 1. However, if it is a probabilistic computer, then there is a possibility of it being in any one of a number of different states. We can describe this probabilistic state by eight nonnegative numbers A,B,C,D,E,F,G,H (where A = probability computer is in state 000, B = probability computer is in state 001, etc.). There is a restriction that these probabilities sum to 1.
different three-bit strings 000, 001, 010, 011, 100, 101, 110, 111. If it is a deterministic computer, then it is in exactly one of these states with probability 1. However, if it is a probabilistic computer, then there is a possibility of it being in any one of a number of different states. We can describe this probabilistic state by eight nonnegative numbers A,B,C,D,E,F,G,H (where A = probability computer is in state 000, B = probability computer is in state 001, etc.). There is a restriction that these probabilities sum to 1.The state of a three-qubit quantum computer is similarly described by an eight-dimensional vector (a,b,c,d,e,f,g,h), called a ket. However, instead of adding to one, the sum of the squares of the coefficient magnitudes,
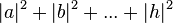 , must equal one. Moreover, the coefficients can have complex values.
Since the absolute square of these complex-valued coefficients denote
probability amplitudes of given states, the phase between any two
coefficients (states) represents a meaningful parameter, which presents a
fundamental difference between quantum computing and probabilistic
classical computing.[12]
, must equal one. Moreover, the coefficients can have complex values.
Since the absolute square of these complex-valued coefficients denote
probability amplitudes of given states, the phase between any two
coefficients (states) represents a meaningful parameter, which presents a
fundamental difference between quantum computing and probabilistic
classical computing.[12]If you measure the three qubits, you will observe a three-bit string. The probability of measuring a given string is the squared magnitude of that string's coefficient (i.e., the probability of measuring 000 =
 , the probability of measuring 001 =
, the probability of measuring 001 =  , etc..). Thus, measuring a quantum state described by complex coefficients (a,b,...,h) gives the classical probability distribution
, etc..). Thus, measuring a quantum state described by complex coefficients (a,b,...,h) gives the classical probability distribution  and we say that the quantum state "collapses" to a classical state as a result of making the measurement.
and we say that the quantum state "collapses" to a classical state as a result of making the measurement.Note that an eight-dimensional vector can be specified in many different ways depending on what basis is chosen for the space. The basis of bit strings (e.g., 000, 001, ..., 111) is known as the computational basis. Other possible bases are unit-length, orthogonal vectors and the eigenvectors of the Pauli-x operator. Ket notation is often used to make the choice of basis explicit. For example, the state (a,b,c,d,e,f,g,h) in the computational basis can be written as:
The computational basis for a single qubit (two dimensions) is
 and
and 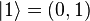 .
.Using the eigenvectors of the Pauli-x operator, a single qubit is
 and
and  .
.Operation
| Is a universal quantum computer sufficient to efficiently simulate an arbitrary physical system? |
 ,
corresponding to the vector (1,0,0,0,0,0,0,0). In classical randomized
computation, the system evolves according to the application of stochastic matrices, which preserve that the probabilities add up to one (i.e., preserve the L1 norm). In quantum computation, on the other hand, allowed operations are unitary matrices, which are effectively rotations (they preserve that the sum of the squares add up to one, the Euclidean or L2 norm).
(Exactly what unitaries can be applied depend on the physics of the
quantum device.) Consequently, since rotations can be undone by rotating
backward, quantum computations are reversible.
(Technically, quantum operations can be probabilistic combinations of
unitaries, so quantum computation really does generalize classical
computation. See quantum circuit for a more precise formulation.)
,
corresponding to the vector (1,0,0,0,0,0,0,0). In classical randomized
computation, the system evolves according to the application of stochastic matrices, which preserve that the probabilities add up to one (i.e., preserve the L1 norm). In quantum computation, on the other hand, allowed operations are unitary matrices, which are effectively rotations (they preserve that the sum of the squares add up to one, the Euclidean or L2 norm).
(Exactly what unitaries can be applied depend on the physics of the
quantum device.) Consequently, since rotations can be undone by rotating
backward, quantum computations are reversible.
(Technically, quantum operations can be probabilistic combinations of
unitaries, so quantum computation really does generalize classical
computation. See quantum circuit for a more precise formulation.)Finally, upon termination of the algorithm, the result needs to be read off. In the case of a classical computer, we sample from the probability distribution on the three-bit register to obtain one definite three-bit string, say 000. Quantum mechanically, we measure the three-qubit state, which is equivalent to collapsing the quantum state down to a classical distribution (with the coefficients in the classical state being the squared magnitudes of the coefficients for the quantum state, as described above), followed by sampling from that distribution. Note that this destroys the original quantum state. Many algorithms will only give the correct answer with a certain probability. However, by repeatedly initializing, running and measuring the quantum computer, the probability of getting the correct answer can be increased.
For more details on the sequences of operations used for various quantum algorithms, see universal quantum computer, Shor's algorithm, Grover's algorithm, Deutsch-Jozsa algorithm, amplitude amplification, quantum Fourier transform, quantum gate, quantum adiabatic algorithm and quantum error correction.
Potential
Integer factorization is believed to be computationally infeasible with an ordinary computer for large integers if they are the product of few prime numbers (e.g., products of two 300-digit primes).[13] By comparison, a quantum computer could efficiently solve this problem using Shor's algorithm to find its factors. This ability would allow a quantum computer to decrypt many of the cryptographic systems in use today, in the sense that there would be a polynomial time (in the number of digits of the integer) algorithm for solving the problem. In particular, most of the popular public key ciphers are based on the difficulty of factoring integers (or the related discrete logarithm problem, which can also be solved by Shor's algorithm), including forms of RSA. These are used to protect secure Web pages, encrypted email, and many other types of data. Breaking these would have significant ramifications for electronic privacy and security.However, other existing cryptographic algorithms do not appear to be broken by these algorithms.[14][15] Some public-key algorithms are based on problems other than the integer factorization and discrete logarithm problems to which Shor's algorithm applies, like the McEliece cryptosystem based on a problem in coding theory.[14][16] Lattice-based cryptosystems are also not known to be broken by quantum computers, and finding a polynomial time algorithm for solving the dihedral hidden subgroup problem, which would break many lattice based cryptosystems, is a well-studied open problem.[17] It has been proven that applying Grover's algorithm to break a symmetric (secret key) algorithm by brute force requires time equal to roughly 2n/2 invocations of the underlying cryptographic algorithm, compared with roughly 2n in the classical case,[18] meaning that symmetric key lengths are effectively halved: AES-256 would have the same security against an attack using Grover's algorithm that AES-128 has against classical brute-force search (see Key size). Quantum cryptography could potentially fulfill some of the functions of public key cryptography.
Besides factorization and discrete logarithms, quantum algorithms offering a more than polynomial speedup over the best known classical algorithm have been found for several problems,[19] including the simulation of quantum physical processes from chemistry and solid state physics, the approximation of Jones polynomials, and solving Pell's equation. No mathematical proof has been found that shows that an equally fast classical algorithm cannot be discovered, although this is considered unlikely. For some problems, quantum computers offer a polynomial speedup. The most well-known example of this is quantum database search, which can be solved by Grover's algorithm using quadratically fewer queries to the database than are required by classical algorithms. In this case the advantage is provable. Several other examples of provable quantum speedups for query problems have subsequently been discovered, such as for finding collisions in two-to-one functions and evaluating NAND trees.
Consider a problem that has these four properties:
- The only way to solve it is to guess answers repeatedly and check them,
- The number of possible answers to check is the same as the number of inputs,
- Every possible answer takes the same amount of time to check, and
- There are no clues about which answers might be better: generating possibilities randomly is just as good as checking them in some special order.
For problems with all four properties, the time for a quantum computer to solve this will be proportional to the square root of the number of inputs. That can be a very large speedup, reducing some problems from years to seconds. It can be used to attack symmetric ciphers such as Triple DES and AES by attempting to guess the secret key.
Grover's algorithm can also be used to obtain a quadratic speed-up over a brute-force search for a class of problems known as NP-complete.
Since chemistry and nanotechnology rely on understanding quantum systems, and such systems are impossible to simulate in an efficient manner classically, many believe quantum simulation will be one of the most important applications of quantum computing.[20]
There are a number of technical challenges in building a large-scale quantum computer, and thus far quantum computers have yet to solve a problem faster than a classical computer. David DiVincenzo, of IBM, listed the following requirements for a practical quantum computer:[21]
- scalable physically to increase the number of qubits;
- qubits can be initialized to arbitrary values;
- quantum gates faster than decoherence time;
- universal gate set;
- qubits can be read easily.
Quantum decoherence
One of the greatest challenges is controlling or removing quantum decoherence. This usually means isolating the system from its environment as interactions with the external world cause the system to decohere. However, other sources of decoherence also exist. Examples include the quantum gates, and the lattice vibrations and background nuclear spin of the physical system used to implement the qubits. Decoherence is irreversible, as it is non-unitary, and is usually something that should be highly controlled, if not avoided. Decoherence times for candidate systems, in particular the transverse relaxation time T2 (for NMR and MRI technology, also called the dephasing time), typically range between nanoseconds and seconds at low temperature.[12]These issues are more difficult for optical approaches as the timescales are orders of magnitude shorter and an often-cited approach to overcoming them is optical pulse shaping. Error rates are typically proportional to the ratio of operating time to decoherence time, hence any operation must be completed much more quickly than the decoherence time.
If the error rate is small enough, it is thought to be possible to use quantum error correction, which corrects errors due to decoherence, thereby allowing the total calculation time to be longer than the decoherence time. An often cited figure for required error rate in each gate is 10−4. This implies that each gate must be able to perform its task in one 10,000th of the decoherence time of the system.
Meeting this scalability condition is possible for a wide range of systems. However, the use of error correction brings with it the cost of a greatly increased number of required qubits. The number required to factor integers using Shor's algorithm is still polynomial, and thought to be between L and L2, where L is the number of bits in the number to be factored; error correction algorithms would inflate this figure by an additional factor of L. For a 1000-bit number, this implies a need for about 104 qubits without error correction.[22] With error correction, the figure would rise to about 107 qubits. Note that computation time is about
 or about
or about  steps and on 1 MHz, about 10 seconds.
steps and on 1 MHz, about 10 seconds.A very different approach to the stability-decoherence problem is to create a topological quantum computer with anyons, quasi-particles used as threads and relying on braid theory to form stable logic gates.[23][24]

No comments:
Post a Comment