From Wikipedia, the free encyclopedia
(Redirected from Center of gravity)
"Center of gravity" redirects here. For the military concept, see center of gravity (military). For the precise definition, see centers of gravity in non-uniform fields.
In the case of a single rigid body, the center of mass is fixed in relation to the body, and if the body has uniform density, it will be located at the centroid. The center of mass may be located outside the physical body, as is sometimes the case for hollow or open-shaped objects, such as a horseshoe. In the case of a distribution of separate bodies, such as the planets of the Solar System, the center of mass may not correspond to the position of any individual member of the system.
The center of mass is a useful reference point for calculations in mechanics that involve masses distributed in space, such as the linear and angular momentum of planetary bodies and rigid body dynamics. In orbital mechanics, the equations of motion of planets are formulated as point masses located at the centers of mass. The center of mass frame is an inertial frame in which the center of mass of a system is at rest at with respect the origin of the coordinate system.
Contents
History
The concept of "center of mass" in the form of the "center of gravity" was first introduced by the ancient Greek physicist, mathematician, and engineer Archimedes of Syracuse. He worked with simplified assumptions about gravity that amount to a uniform field, thus arriving at the mathematical properties of what we now call the center of mass. Archimedes showed that the torque exerted on a lever by weights resting at various points along the lever is the same as what it would be if all of the weights were moved to a single point — their center of mass. In work on floating bodies he demonstrated that the orientation of a floating object is the one that makes its center of mass as low as possible. He developed mathematical techniques for finding the centers of mass of objects of uniform density of various well-defined shapes.[1]Later mathematicians who developed the theory of the center of mass include Pappus of Alexandria, Guido Ubaldi, Francesco Maurolico,[2] Federico Commandino,[3] Simon Stevin,[4] Luca Valerio,[5] Jean-Charles de la Faille, Paul Guldin,[6] John Wallis, Louis Carré, Pierre Varignon, and Alexis Clairaut.[7]
Newton's second law is reformulated with respect to the center of mass in Euler's first law.[8]
Definition of center of mass
The center of mass is the unique point at the center of a distribution of mass in space that has the property that the weighted position vectors relative to this point sum to zero. In analogy to statistics, the center of mass is the mean location of a distribution of mass in space.A system of particles
In the case of a system of particles Pi, i = 1, …, n , each with mass mi that are located in space with coordinates ri, i = 1, …, n , the coordinates R of the center of mass satisfy the conditionA continuous volume
If the mass distribution is continuous with the density ρ(r) within a volume V, then the integral of the weighted position coordinates of the points in this volume relative to the center of mass R is zero, that isIf a continuous mass distribution has uniform density, which means ρ is constant, then the center of mass is the same as the centroid of the volume.[9]. The center of mass is not the point at which a plane separates the distribution of mass into two equal halves. In analogy with statistics, the median is not the same as the mean.
Barycentric coordinates
Further information: Barycentric_coordinate_system
The coordinates R of the center of mass of a two-particle system, P1 and P2, with masses m1 and m2 is given bySystems with periodic boundary conditions
For particles in a system with periodic boundary conditions two particles can be neighbors even though they are on opposite sides of the system. This occurs often in molecular dynamics simulations, for example, in which clusters form at random locations and sometimes neighboring atoms cross the periodic boundary. When a cluster straddles the periodic boundary, a naive calculation of the center of mass will be incorrect. A generalized method for calculating the center of mass for periodic systems is to treat each coordinate, x and y and/or z, as if it were on a circle instead of a line.[10] The calculation takes every particle's x coordinate and maps it to an angle, can be generated:
can be generated: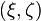 plane, these coordinates lie on a circle of radius xmax. From the collection of
plane, these coordinates lie on a circle of radius xmax. From the collection of  and
and  values from all the particles, the averages
values from all the particles, the averages  and
and  are calculated. These values are mapped back into a new angle,
are calculated. These values are mapped back into a new angle,  , from which the x coordinate of the center of mass can be obtained:
, from which the x coordinate of the center of mass can be obtained: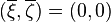 , then
, then  is undefined. This is a correct result, because it only occurs when all
particles are exactly evenly spaced. In that condition, their x coordinates are mathematically identical in a periodic system.
is undefined. This is a correct result, because it only occurs when all
particles are exactly evenly spaced. In that condition, their x coordinates are mathematically identical in a periodic system.Center of gravity
Center of gravity is the point in a body around which the resultant torque due to gravity forces vanish. Near the surface of the earth, where the gravity acts downward as a parallel force field, the center of gravity and the center of mass are the same.The study of the dynamics of aircraft, vehicles and vessels assumes that the system moves in near-earth gravity, and therefore the terms center of gravity and center of mass are used interchangeably.
In physics the benefits of using the center of mass to model a mass distribution can be seen by considering the resultant of the gravity forces on a continuous body. Consider a body of volume V with density ρ(r) at each point r in the volume. In a parallel gravity field the force f at each point r is given by,
By selecting the center of gravity as the reference point for a rigid body, the gravity forces will not cause the body to rotate, which means weight of the body can be considered to be concentrated at the center of mass.
Linear and angular momentum
The linear and angular momentum of a collection of particles can be simplified by measuring the position and velocity of the particles relative to the center of mass. Let the system of particles Pi, i=1,...,n be located at the coordinates ri and velocities vi. Select a reference point R and compute the relative position and velocity vectors,Locating the center of mass
Main article: Locating the center of mass
The experimental determination of the center of mass of a body uses
gravity forces on the body and relies on the fact that in the parallel
gravity field near the surface of the earth the center of mass is the
same as the center of gravity.The center of mass of a body with an axis of symmetry and constant density must lie on this axis. Thus, the center of mass of a circular cylinder of constant density has its center of mass on the axis of the cylinder. In the same way, the center of mass of a spherically symmetric body of constant density is at the center of the sphere. In general, for any symmetry of a body, its center of mass will be a fixed point of that symmetry.[12]
In two dimensions
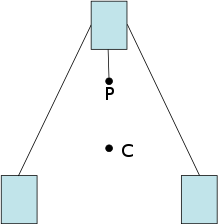
An experimental method for locating the center of mass is to suspend the object from two locations and to drop plumb lines from the suspension points. The intersection of the two lines is the center of mass.[13]The shape of an object might already be mathematically determined, but it may be too complex to use a known formula. In this case, one can subdivide the complex shape into simpler, more elementary shapes, whose centers of mass are easy to find. If the total mass and center of mass can be determined for each area, then the center of mass of the whole is the weighted average of the centers.[14] This method can even work for objects with holes, which can be accounted for as negative masses.[15]
A direct development of the planimeter known as an integraph, or integerometer, can be used to establish the position of the centroid or center of mass of an irregular two-dimensional shape. This method can be applied to a shape with an irregular, smooth or complex boundary where other methods are too difficult. It was regularly used by ship builders to compare with the required displacement and centre of buoyancy of a ship, and ensure it would not capsize.[16][17]
In three dimensions
An experimental method to locate the three dimensional coordinates of the center of mass begins by supporting the object at three points and measuring the forces, F1, F2, and F3 that resist the weight of the object, W= −Wk (k is the unit vector in the vertical direction). Let r1, r2, and r3 be the position coordinates of the support points, then the coordinates R of the center of mass satisfy the condition that the resultant torque is zero,Applications
Aeronautics
Main article: Center of gravity of an aircraft
The center of mass is an important point on an aircraft,
which significantly affects the stability of the aircraft. To ensure
the aircraft is stable enough to be safe to fly, the center of mass must
fall within specified limits. If the center of mass is ahead of the
forward limit, the aircraft will be less maneuverable, possibly to the
point of being unable to rotate for takeoff or flare for landing.[19]
If the center of mass is behind the aft limit, the aircraft will be
more maneuverable, but also less stable, and possibly so unstable that
it is impossible to fly. The moment arm of the elevator will also be reduced, which makes it more difficult to recover from a stalled condition.[20]For helicopters in hover, the center of mass is always directly below the rotorhead. In forward flight, the center of mass will move aft to balance the negative pitch torque produced by applying cyclic control to propel the helicopter forward; consequently a cruising helicopter flies "nose-down" in level flight.
Astronomy
Main article: Barycentric coordinates (astronomy)
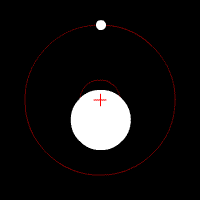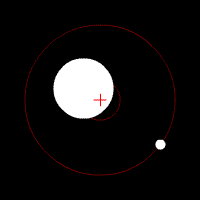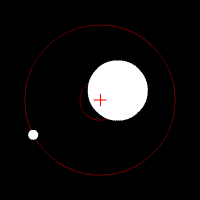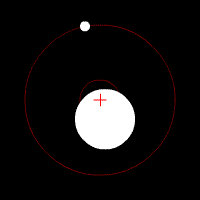
The center of mass plays an important role in astronomy and astrophysics, where it is commonly referred to as the barycenter.
The barycenter is the point between two objects where they balance each
other; it is the center of mass where two or more celestial bodies orbit each other. When a moon orbits a planet, or a planet orbits a star, both bodies are actually orbiting around a point that lies away from the center of the primary (larger) body.[21] For example, the Moon does not orbit the exact center of the Earth,
but a point on a line between the center of the Earth and the Moon,
approximately 1,710 km (1062 miles) below the surface of the Earth,
where their respective masses balance. This is the point about which the
Earth and Moon orbit as they travel around the Sun. If the masses are more similar, e.g., Pluto and Charon, the barycenter will fall outside both bodies.

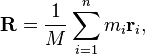

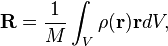




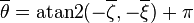

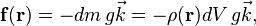










No comments:
Post a Comment